Vector math

Pictorus implements Vectors similarly to Numpy and Matlab. Vectors can be transformed by other vectors, and they can also be transformed by scalars.

This is because under the hood, all signals in Pictorus are stored as 2d vectors. So, when we speak of "scalars", we simply mean a signal stored like [[3.14159]]. Similarly, a "vector" is stored as [[1, 2, 3]]. We also support "2d vectors" (sometimes called matrices) like [[1, 2], [3, 4], [5, 6]]. We don't currently support 3d or higher dimension vectors (but plan to).

The benefit of storing everything as a 2d vector is it makes it relatively easy to perform operations on any two signals, whether they are scalars, vectors, or matrices.

Creating vectors

There is currently only one, fairly annoying way to create a new vector, using the Vector Merge block, which creates a flat vector from inputs. This is often in conjunction with a Vector Reshape block. For example, a simple 3x3 identity matrix can be constructed with:

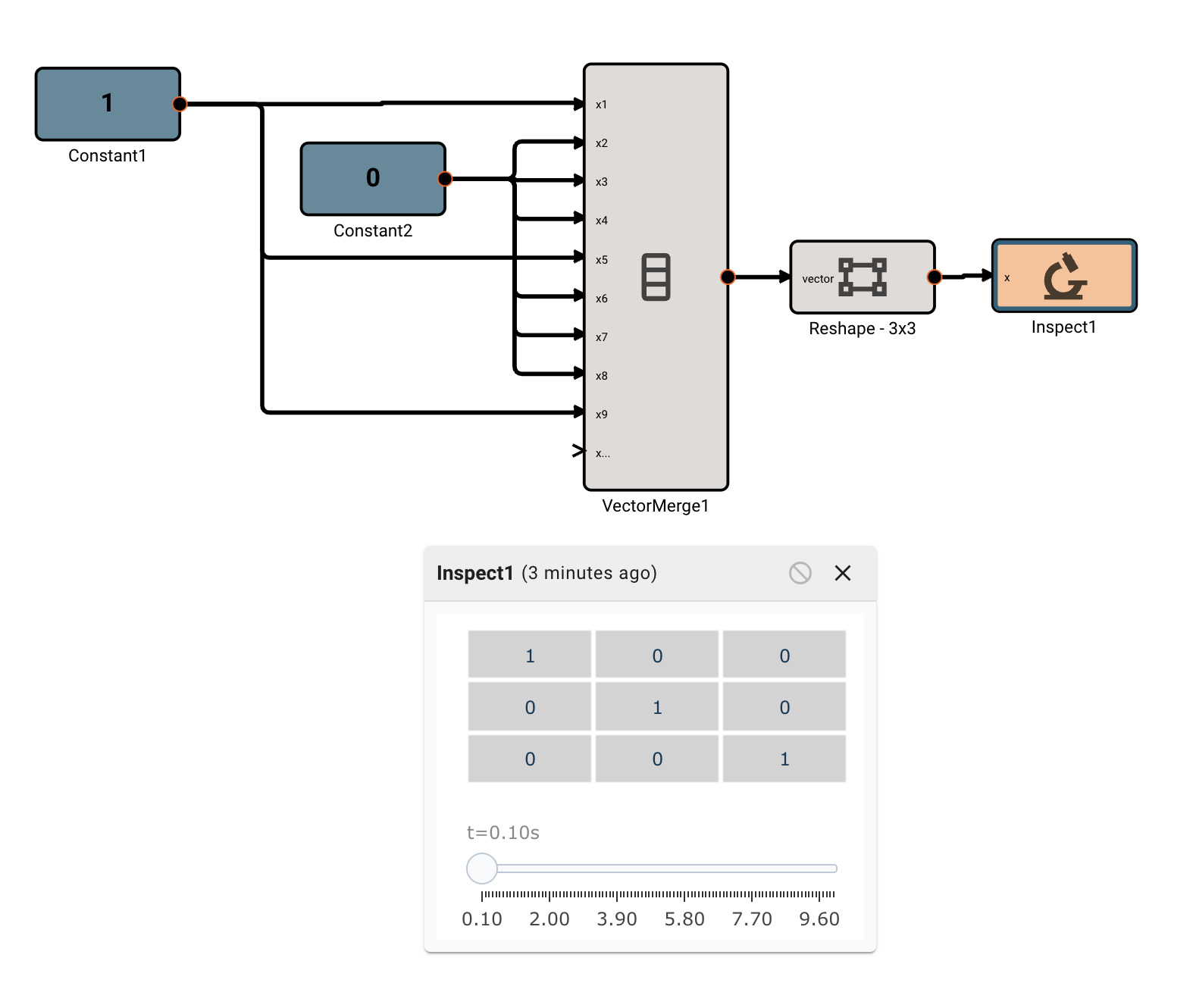
As mentioned, we can operate on scalars and vectors pretty easily - as long as we don't violate any dimensional rules of the operation involved. For example, we can scale the Identity matrix by a scalar factor of 10, and then subtract a scalar like so, and it applies to the entire vector:

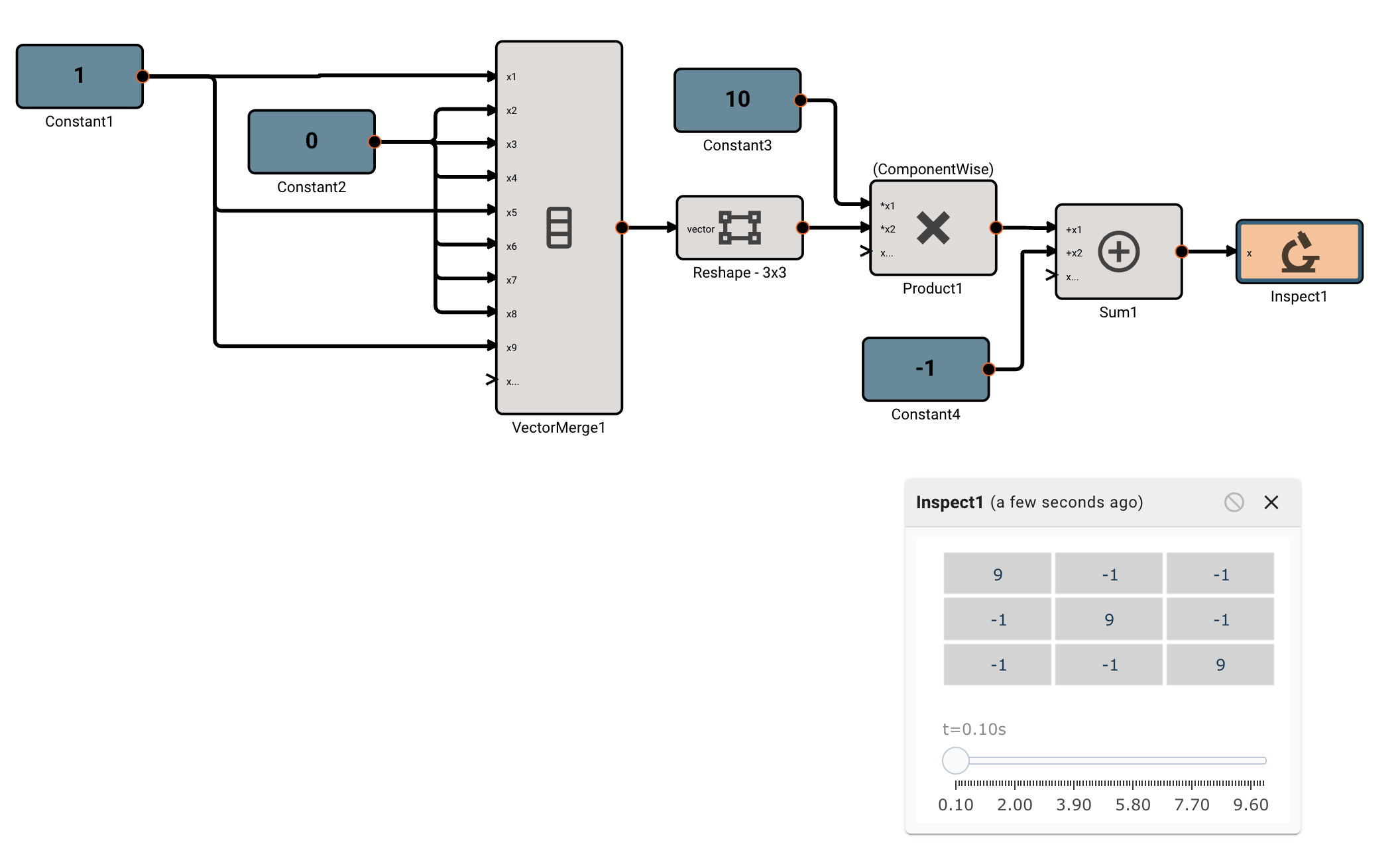
Vector sizing rules

Certain vector operations have firm vector size requirements. A few common ones to be aware of:

• When using the Matrix Multiplication method of the Product Block, the inner dimensions of the input vectors must match. For example, a 2x3 vector can matrix multiply with a 3x4 matrix, since the inner dimensions are both 3. The order of the product inputs clearly matters here.
• The Cross Product block only works for 1x3 or 3x1 sized vectors.
• When using the Inverse method of the Matrix Inverse block, the input block must be square (rows == cols).
• The Determinant block also requires square matrices.

What about the overhead involved with this paradigm?

Storing everything as double precision 2d vectors is certainly not cheap, computationally. For the most part, the fact that Pictorus diagrams compile to highly performant Rust apps leveraging the nalgebra crate means our apps are still generally very efficient. But eventually, we intend to add a precompile step to the code generator that will strip down vectors to scalars where appropriate, and reduce floating point precision if specified by the users. If you are encountering a significant performance issue, please reach out and we'd love to dive into it!