Transfer Function Block

This block is experimental at this time

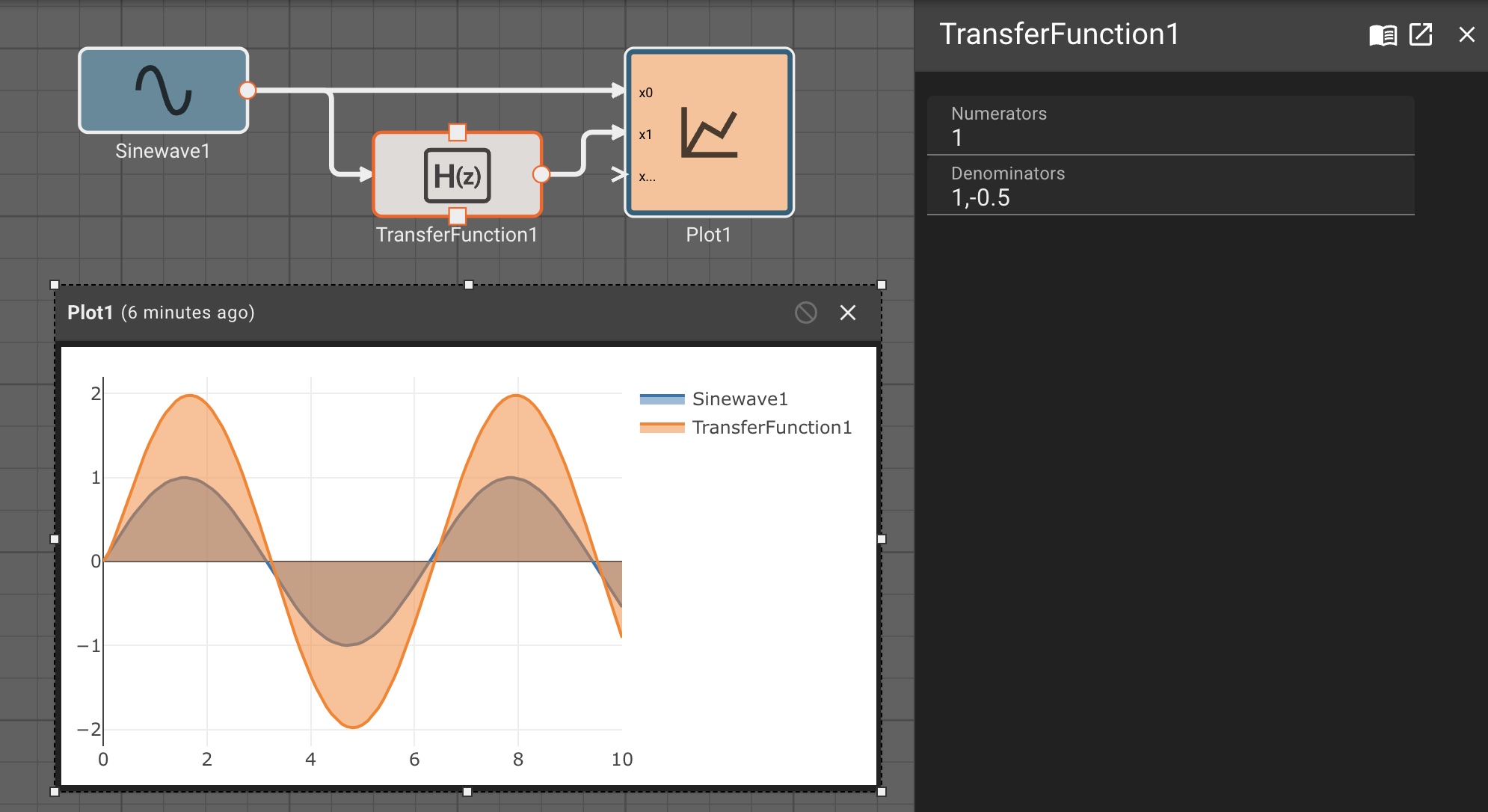
The Transfer Function block emits the discrete Transfer Function of the input signal, determined by numerator and denominator coefficients specified in block parameters.

A transfer function is defined as H(z) = Y(z) / X(z) and the numerator and denominator coefficients are used to compute the output of the block:

y[n] = b[0] * x[n] + b[1] * x[n-1] + ... + b[n] * x[n-N] - a[1] * y[n-1] - a[2] * y[n-2] + ... - a[n] * y[n-N].

Where the b[...] are the numerator coefficients and a[...] are the denominator coefficients. Care must be taken when choosing denominator coefficients to avoid unstable systems. The Transfer function is fundamentally the ratio between the output and the input signals. As such, the default numerator and denominator coefficients of 1.0 will simply emit the input signal by default.

A transfer function that represents a decay of 1/2 each time step can be represented as:

H(z) = Y(z) / X(z) = z / (z - 0.5).

The numerator would be [1] and the denominator would be [1, -0.5].

The numerator and denominator must have dimensions of at least 1 and the 0th value of the denominator will be skipped (but must be present), as it represents the coefficient for y[n], the current output.

Parameters

• Denominators (default = [1])
• Numerators (default = [1])

Examples